מטריצות
17/10/2020
מה זה בכלל מטריצה?
האופן הכי בסיסי שאפשר לתאר מטריצה - טבלה של מספרים. פשוט כמות מסויימת של שורות ועמודות שבכל אחת מהן יש מספר כלשהו. כמובן, שאפשר להשתמש במטריצות שבכל מיקום בהן יש אובייקטים אחרים, אבל למי שזה נשמע מסובך מדי, שיעזוב את זה, כי מטריצות עם מספרים הוא השימוש הכי בסיסי והכי נפוץ. הנה כמה דוגמאות למטריצות:
מטריצה ריבועית עם מספרים טבעיים: \[\begin{pmatrix} 2&3\\ 1&7 \end{pmatrix}\] מטריצה בגודל 2 על 3: \[\begin{pmatrix} 4.15&-2.97&-1.15\\ -3.2&-2.74&5.67 \end{pmatrix}\] מטריצה בגודל 1 על 4: \[\begin{pmatrix} 0\\ 0\\ 0\\ 1 \end{pmatrix} \]אז כמו שראיתם, את המטריצה מייצגים בדרך כלל בסידור המספרים (או כמו שלפעמים קוראים למיקומים במטריצה ״כניסות״) בשורות ועמודות, ואת הכל עוטפים בסוגריים גדולים. (יש מקומות שמשתמשים בסוגריים מרובעים כמו בדוגמה למטה)
\[\begin{bmatrix} 3&-1&5\\ 0&4&-4\\ 1&7&3 \end{bmatrix} \]אוקי סבבה, אז מה העניין פה?
מטריצה היא אובייקט מתמטי שיש לו הרבה שימושים. אחד הנפוצים שבהם הוא ייצוג של טרנספורמציות לינאריות. לא להיבהל, זה לא באמת כזה מסובך..
בשביל להבין מה היא טרנספורמציה לינארית נתחיל מלהסתכל על איזשהו מישור וכדי שתהיה לנו נקודת ייחוס, נגדיר קורדינטות וראשית צירים (שכולנו מכירים טוב טוב מהתיכון):

באופן ספציפי למישור שאנחנו מדברים עליו, טרנספורמציה ממפה קבוצה של נקודות לקבוצה אחרת של נקודות, כל נקודה ,״תעבור״ לנקודה אחרת המתאימה לה. זאת בעצם פונקציה שכאשר נותנים לה נקודה כקלט - מקבלים נקודה חדשה כפלט. היא בעצם מעבירה (או מעתיקה) את הנקודות ממיקום אחד - למיקום אחר, לכן קוראים לה טרנספורמציה (בעברית: התמרה, או העתקה).
מה הקטע עם הלינאריות?
כשאנחנו מדברים על טרנספורמציה לינארית, אנחנו מצמצמים קצת (הרבה) את קבוצת הטרנספורמציות (שעד עכשיו לא היה עליהן שום אילוץ) לקבוצה פשוטה יחסית. קבוצת הטרנספורמציות הלינאריות היא קבוצה ששומרת על חיבור וכפל בסקלר. מה זאת אומרת? שאם מחברים שתי נקודות לפני הטרנספורמציה (עוד שנייה נסביר איך מחברים שתי נקודות או מכפילים) ואז מפעילים את הטרנספורמציה על התוצאה, נגיע לאותה נקודה שנקבל אם נפעיל את הטרנספורמציה על כל אחת מהנקודות בנפרד ואז נחבר אותן. כלומר, הסדר של הפעולות לא ממש משנה. קצת הרבה מילים, אז אולי יהיה הפעם יותר נוח לראות את זה אלגברית:
\[\begin{eqnarray} &T(v)+T(u) = T(v+u)\\ &a\cdot{}T(v) = T(a\cdot{}v) \end{eqnarray}\]אלה תכונות מעניינות שעוזרות לנו מאוד בהרבה מקרים, אבל כרגע מה שמעניין זה שמדובר בטרנספורמציות פשוטות יחסית ושכל טרנספורציה כזאת אפשר לייצג על-ידי מטריצה.
הבטחתי שאסביר איך מחברים נקודות במישור, אז זה מאוד פשוט - מחברים את הערך בכל אחת מהקורדינטות שלהם (ובשביל להכפיל, מכפילים כל אחת מהקורדינטות):
\[\begin{eqnarray} &(1,2)+(3,4)=(4,6)\\ &5\cdot{}(2,3) = (10,15) \end{eqnarray}\]אבל בעצם, יותר נכון להייחס לנקודות במישור כווקטורים. אפשר לייצג וקטורים בצורה גרפית כחיצים המצביעים מהראשית אל הנקודה אליה אנחנו מתייחסים, נניח הנקודה (1,2) תיוצג על-ידי הוקטור:

אז אנחנו יודעים מה זה טרנספורמציה, אבל איך מתארים אחת כזאת? אי אפשר הרי לרשום במפורש לכל נקודה איזה נקודה מתאימה לה:
\[ \begin{eqnarray} &(1,2)\rightarrow{}(5,4)\\ &(3,4)\rightarrow{}(-1,2)\\ &(-7,13)\rightarrow{}(-2,3)\\ &(5,3)\rightarrow{}(-3,8)\\ &(1,9)\rightarrow{}(-9,6)\\ &\vdots{}\quad\vdots{}\quad\vdots{}\quad\vdots{} \end{eqnarray} \]הרי יש אינסוף נקודות, אז לא נסיים אף פעם.. אז מה שעושים זה מייצגים כל וקטור במישור על ידי וקטורי בסיס. וקטורי בסיס הם וקטורים סטנדרטיים, בגודל 1 הנמצאים על הצירים של מערכת הצירים ומסמנים אותם בסימון $e_1$ ו- $e_2$. זה נראה ככה:

כשיש לנו את וקטורי הבסיס, אפשר לייצג כל וקטור במישור על ידי צירוף שלהם, לדוגמה:

זה יחסית טריוויאלי, אין פה איזה משהו עמוק אז אל תחפשו יותר מדי.
ככה אפשר לרשום את הוקטור (5,3) על ידי $v=5\cdot{}e_1+3\cdot{}e_2$. בגלל שהטרנספורמציה שאנחנו מפעילים על הוקטור היא לינארית, במקום לחשב את $T(v)$, כלומר, את הטרנספורמציה ישר על הוקטור $v$ נוכל לחשב:
\[ \begin{eqnarray} &T(v)=5\cdot{}T(e_1)+3\cdot{}T(e_2) \end{eqnarray} \]נוכל לעשות את זה לכל וקטור (ולא רק ל (5,3)) אז כל מה שאנחנו צריכים לשמור בשביל לייצג את הטרנספורמציה הוא לאן הולכים וקטורי הבסיס, משם נוכל כבר לחשב את הטרנספורמציה על כל וקטור במישור כמו שעשינו על (5,3).
ועכשיו איך מייצגים לאן הולכים וקטורי הבסיס?
כאן המטריצות נכנסות לתמונה, מסדרים את הוקטורים שאליהם מועתקים וקטורי הבסיס בתור העמודות של המטריצה. למה דווקא עמודות? זה נגזר מאיך שמוגדרת מכפלת מטריצות אז אם זה מציק לכם ואתם רוצים להעמיק, לכו לקרוא על זה, בכל אופן, תראו איך זה עובד:
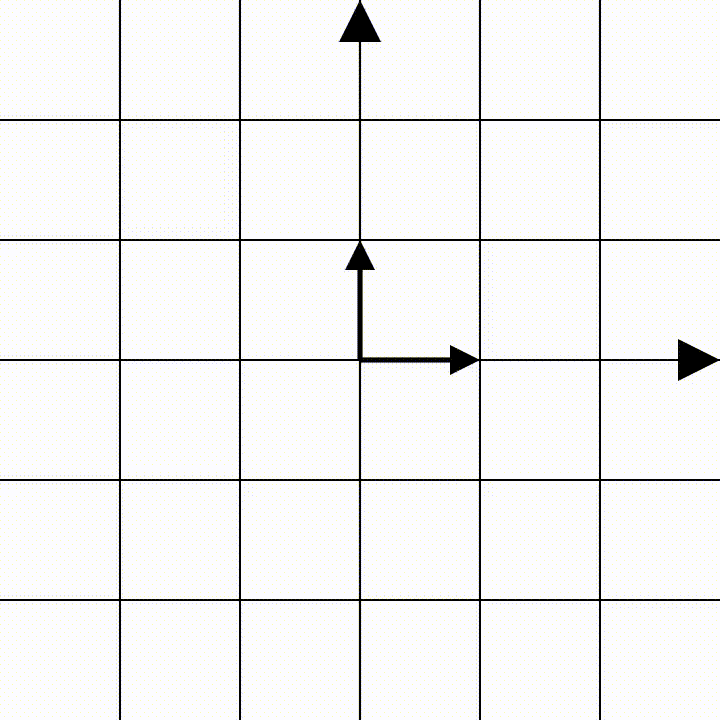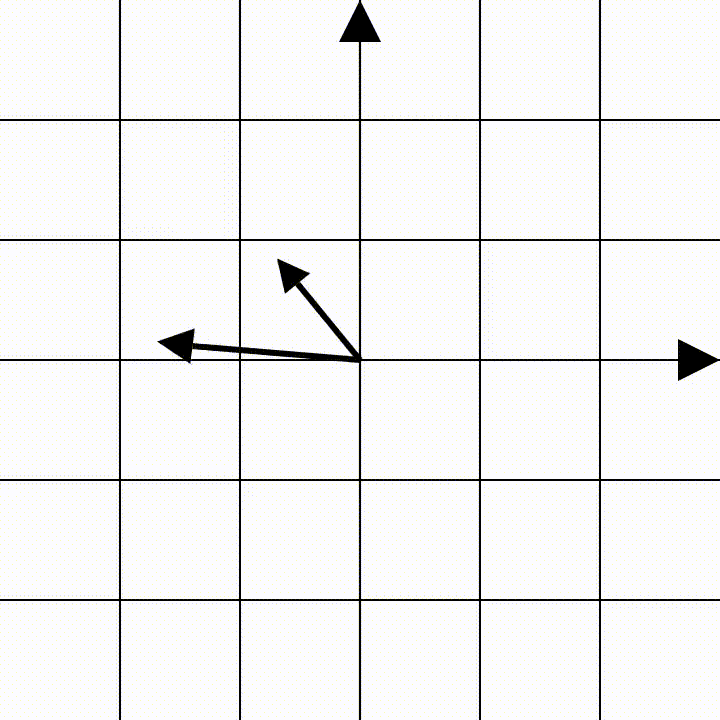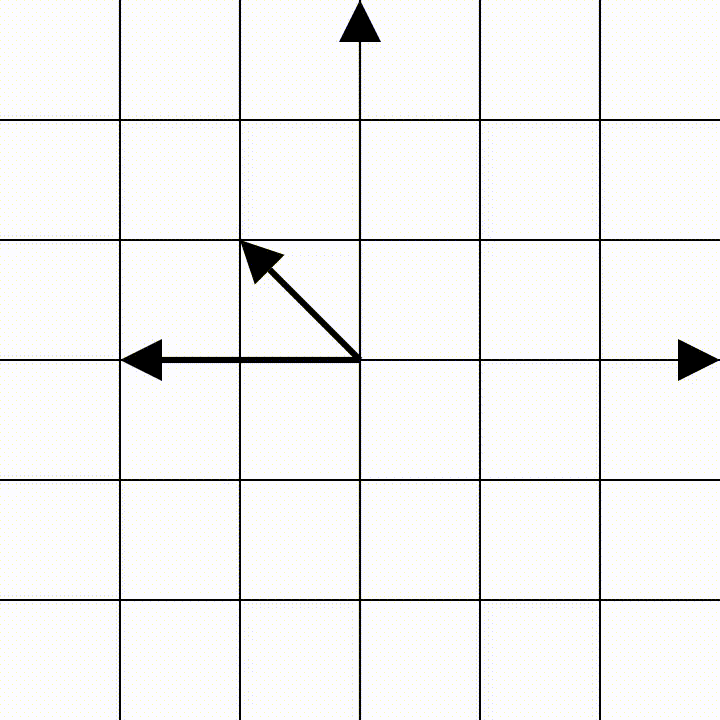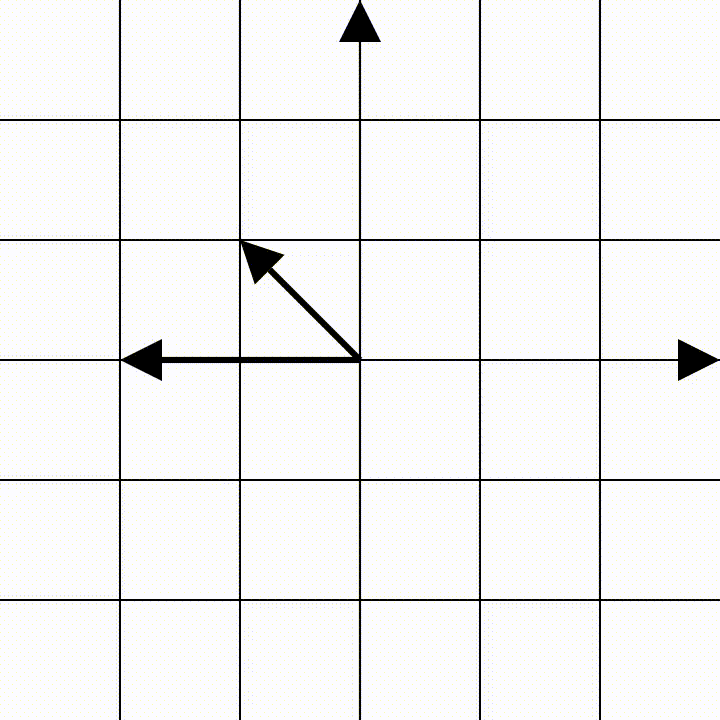
את הטרנספורמציה הזאת נייצג על ידי המטריצה הזאת:
\[\begin{pmatrix} -1&-2\\ 1&0 \end{pmatrix}\]ממליץ לבהות בזה שנייה, ולראות איך הוקטור $e_1=(1,0)$ מועתק למיקום החדש שלו והופך לוקטור $(-1,1)$, זה גם הוקטור שהעמודה הראשונה במטריצה מייצגת. ואיך הוקטור $e_2=(0,1)$ הופך ל- $(-2,0)$ . שני הוקטורים האלה עברו טרנספורמציה לינארית, ובגלל שהם פורשים את כל המישור, כלומר, שניתן לייצג באמצעותם כל וקטור במישור, אז הם מתארים באופן מוחלט את הטרנספורמציה לכל נקודה במישור.
המשמעות של זה היא שאפשר להציג את זה ככה שכל המישור עובר את הטרנספורמציה, אז הדוגמה הבאה ממחישה איך כל נקודה עוברת למיפוי שלה לפי הטרנספורמציה שהמטריצה הקודמת מתארת:

מה עם מטריצות עם יותר שורות או עמודות?
טוב אלה פשוט טרנספורמציות שפועלות במרחבים ממימדים יותר גבוהים, ואפשר אולי להסביר את זה כאשר מדברים על מרחבים עם שלושה מימדים, אבל מעל זה, זה כבר מסתבך וקשה לראות את זה באופן גרפי. אבל שלא תטעו - למטריצות ממימדים גבוהים יש הרבה מאוד שימושים, למעשה, רוב השימושים שעושים עם מטריצות הם לא בדו-מימד.
נסיים את הפוסט בלהראות כמה דוגמאות לטרנספורציות לינאריות ולמטריצות שמייצגות אותן כדי שתקבלו עוד קצת תחושה על הנושא:
דוגמה ראשונה:
\[\begin{pmatrix} 1&-1\\ 1&1 \end{pmatrix}\]נראית ככה:

דוגמה שניה:
\[\begin{pmatrix} -2&1\\ 2&-1 \end{pmatrix}\]דוגמה שלישית:
 \[\begin{pmatrix}
3&0\\
0&-2
\end{pmatrix}\]
\[\begin{pmatrix}
3&0\\
0&-2
\end{pmatrix}\]
